主管：中国科学院
主办：中国优选法统筹法与经济数学研究会
　　　中国科学院科技战略咨询研究院
Chinese Journal of Management Science

Chinese Journal of Management Science >

2024 , Vol. 32 >Issue 11: 222 - 232

DOI: https://doi.org/10.16381/j.cnki.issn1003-207x.2022.0859

Study on Cooperative Strategy of Government-enterprise Joint Reserve of Emergency Supplies

  • Sheng Li 1, 2 ,
  • Jingchun Feng , 2 ,
  • Kaili Wu 2 ,
  • Ke Zhang 2
Expand
  • 1. College of Civil Engineering，Nanjing Forestry University，Nanjing 210037，China
  • 2. Business School，Hohai University，Nanjing 211100，China

Received date: 2022-04-22

  Revised date: 2022-07-04

  Online published: 2024-12-09

Fold

Abstract

A supply system is studied in which the government， core suppliers and node suppliers jointly reserve emergency supplies.On the basis of establishing the principal-agent relationship between government and enterprise， two forms of cost sharing contract are proposed： （1） Reserve cost sharing contract， which is a kind of classical cost sharing mechanism， that is， the dominant core supplier in the supply chain unilaterally shares part of the reserve cost of the node supplier； （2） Bilateral cost-sharing contract with revenue sharing， that is， core suppliers share fixed proportion of reserve revenue and reward and punishment revenue with node suppliers， and at the same time， two suppliers share certain proportion of reserve cost for each other， forming a two-way subsidy mechanism.By means of differential game， the optimal decision-making strategy of government and enterprise is deduced. Finally， combined with numerical simulation， the differential effects of purchase price and other parameters on equilibrium strategy and Fed inventory under two contract forms are investigated， and some management implications are obtained. The results show that：（1） Compared with the classical CS contract with unilateral compensation mechanism as the core， RS&BS contract enables the government to have a larger range of executable purchase price by introducing revenue sharing and bilateral compensation mechanism；（2） The cooperation form of suppliers will also reverse the government's pricing strategy. Under THE RS&BS contract， the sharing strategy of the core supplier only depends on the revenue distribution within the supplier， while under the CS contract， its sharing strategy is restricted by the external purchase price.（3） CS contract and RS&BS contract have their own best application scenarios. The CS contract can increase the quantity and reserve efficiency of the Fed's inventory. RS&BS contracts are more helpful in keeping inventories at a stable and safe level.

Key words： emergency supply chain; government-enterprise joint; materials reserves; cost sharing contract

Cite this article

Sheng Li , Jingchun Feng , Kaili Wu , Ke Zhang . Study on Cooperative Strategy of Government-enterprise Joint Reserve of Emergency Supplies[J]. Chinese Journal of Management Science, 2024 , 32(11) : 222 -232 . DOI: 10.16381/j.cnki.issn1003-207x.2022.0859

1 引言

频繁发生的灾害事件给人民生命和财产安全造成了严重的损害，而充足的应急物资储备是降低灾害损失的有效手段。为应对突发灾害事件，政府通常会事前储备一定数量的应急物资，但由于资金限制以及灾害发生时的物资需求激增，政府难以仅依靠自身在事前储备充足的应急物资。为此，开展政企联合储备工作，依靠企业代储一定数量的应急物资，是完善应急物资保障机制，提升应急管理服务能力的有效手段。但现有政企联合储备研究多局限在政企的一对一供应系统，而忽视了供应商间的合作关系［1］，这使得研究成果缺乏适用性及合理性。因此，有必要在政企委托代理关系的基础上进一步引入供应商间合作关系。考虑到合作的基础是互利共赢，因此，为建立供应商之间的良性合作关系，本文为供应商设计了两类契约协调机制，并在时间维度上考察了不同契约下政企以及企业间的合作策略，以期为更好地促进政企各方的合作提供可借鉴的方法与策略。
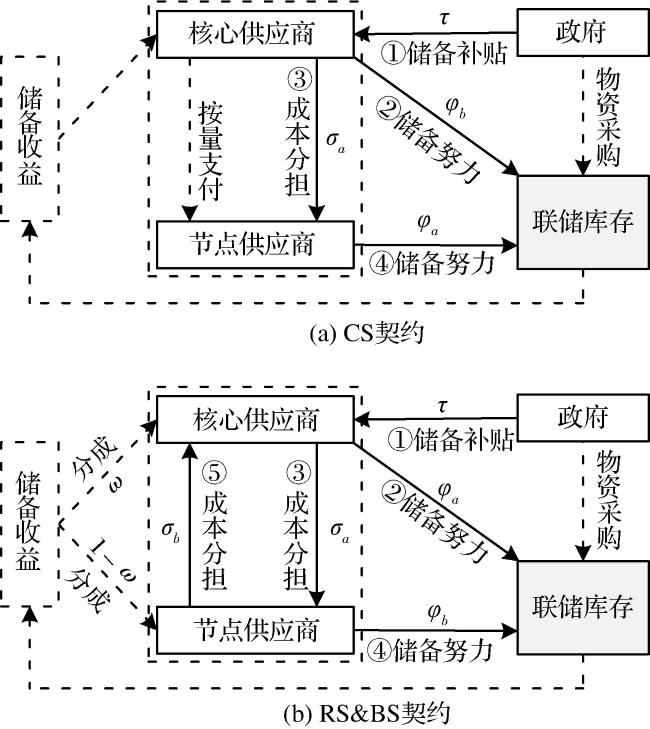
为缓解政府单独储备应急物资时面临的困境，多位学者针对政企联合储备问题开展了研究。吴勇刚等［2］认为，企业在物资储备领域已有成熟商业模式及规范化管理经验，因此，政府应以外包的形式交由企业管理；Zhang等［3］同样认为，政府应与供应商建立长效合作机制以降低储备成本。以上研究均指出，政府应加强与企业的合作，并充分利用企业在商业运营方面的优势。但上述研究均是基于理论层面的定性研究，难以解决操作层面存在的实际问题。基于此，部分学者开展了政府与供应商联合储备物资的策略研究。高晓宁等［4］提出了一种实物代储与生产能力代储相结合的储备系统，并给出了政企双方的最优储备策略。张琳等［5］提出了柔性机制下的政企合作策略，此后，又设计了一个包含基准价格和两种补贴的价格柔性契约，并证明了这一契约对实现政企供应链协调的有效性［6］。上述文献均研究了政府与单一供应商的合作关系，在此基础上，部分学者开始探讨政府与多个供应商合作的场景。刘阳等［7］分析了一个政府与两个竞争型供应商参与的代储供应链，并给出了使供应商利润得到合理分配的期权价格，此后，又设计了政府和两个成本异质性企业组成的物资供应系统，并构建了协调企业利润分配的柔性机制［8］。上述研究虽极大的拓展了政企合作的供应链结构，但是，仍缺乏对供应商间合作关系，特别是对契约机制的探讨。
供应链的契约协调机制是供应链管理的重要内容，已有众多学者开展了相关研究。周艳菊等［9］考虑了具有质量和数量弹性的三级供应链协调问题，并设计了成本分担和收益共享契约以协调该供应链；刘云志和樊治平［10］研究了一个考虑损失规避与产品质量水平的二级供应链，并设计了一个批发价格-质量成本分担契约实现了对供应链的协调；李友东等［11］针对一个受政府碳排放规制的减排供应链协调问题，设计了减排增益分享与减排成本分担两种协调契约，分析表明，减排成本分担契约有助于提高零供两主体的利润，减排增益分享契约仅对零售商单方面有利。通过回顾以上研究可以发现，现有文献中均对成本分担契约进行了一定的研究，但研究内容更多地是将成本分担契约与其他契约进行比较，而缺乏对不同形式成本分担契约的比较。
此外，为进一步研究政企联合储备系统的长期运行效果，有必要将时间因素纳入供应链的协调问题中，以得到其在在时间维度上的特征。关于从时间维度上考察供应链的协调问题，汪勇杰等［12］结合政府补贴机制，构建了基于进化理论的研发外包动态博弈模型，通过分析系统均衡解，将整个演化周期划分为稳定期与混沌期；叶同等［13］对供应链联合减排动态优化与协调问题，提出了一种补助契约，使得制造商和供应商在减排合作周期内实现了Pareto改善；张建军等［14］则采用变分法建立了基于连续时间的供应链声誉微分决策模型，指出长期稳定的合作关系有助于实现供应链协调。
本文在研究过程中充分借鉴和吸收了已有文献，与上述部分文献的联系与创新归纳如下：（1）文献［5，6］均假设政府与单一供应商开展“一对一”合作，本文则将此拓展为政府与供应商“一对二”联合储备供应系统。此外，不同于上述文献仅研究政企间的委托代理关系。本文在此基础上，进一步设计供应商之间的两种成本分担契约，借此考察了供应商间的不同合作形式对政企各方的影响，并实现了对供应链的协调。（2）文献［8］虽然研究了政府与两个供应商联合储备应急物资的情形，但两个供应商之间为非合作的竞争关系，缺乏本文的契约协调机制，且供应商的异质性主要体现在成本参数。而本文中两个供应商的异质性不仅体现在成本参数的不同，还因为两个供应商处于供应链中的不同地位，其与政府的合作形式及获利模式也存在差异。（3）文献［9，11］虽然也探讨了供应商间的成本分担契约，但重在阐述成本分担机制有和无的差异，本文则通过对两种形式的成本分担契约进行比较，重点分析其各自优势及适用场景。
综上所述，本文将供应商间的契约合作关系引入政企委托代理关系中，对现有政企联合储备研究进行了拓展。此外，多数文献构建的都是静态的政企联合储备模型，而本文建立的动态决策模型可更好地考察联合储备策略的长期效果，可从更多视角为政企联合储备工作提供决策建议。

2 问题描述

2.1 概念界定

代储供应商可按自身规模以及在供应链中的主导地位划分为核心供应商与节点供应商。核心供应商一般处于供应链核心位置，多为与政府有长期合作关系的大型企业或政府关联型企业。节点供应商多为中小型厂商，与核心供应商之间多通过各类协议结成优势互补的联盟型组织，政府一般不与其直接签署代储协议。
成本分担是供应商进行合作的一种常见形式，本文提出了两种形式的成本分担契约，分别为：（1）储备成本分担契约（参考文献［13］的命名方式，称为CS契约），这是一类经典的成本分担机制，即由供应链中占主导地位的一方单边分担合作方的部分储备成本；（2）含收益（储备及奖惩收益）分成的双边成本分担契约（RS&BS契约），即核心供应商给予节点供应商固定比例的储备及奖惩收益分成，同时，两个供应商都为对方分担一定比例的储备成本，形成双向补助机制。后文将结合两个模型结果的对比及数值仿真得出两种成本分担契约的理论价值和现实意义。

2.2 模型变量含义与假设条件

为使本文结论具有现实意义，进行如下假设：
（1）供应商努力成本是努力水平的递增凹函数，即供应商提升努力水平所对应的边际成本递增。有 C φ i t = μ i φ i 2 t / 2，满足 C ' φ i t > 0， C ″ φ i t > 0。
（2）政府与供应商签订的是单周期采购契约，契约时长不超过物资保质期。此外，政府仅通过采购的形式从供应商处获取物资，不采取行政措施强行征调物资。
（3）假设政府和供应商均基于完全信息的理性决策，各方在任意时刻都有着相同的正贴现率。
（4）供应商a和供应商b的储备行为直接决定联储库存量 Q s ( t )，政府g通过激励供应商行为间接影响 Q s ( t )，供应商通过施加储备努力，通过转化系数 θ i变为储备物资，并留在库存中。随着时间推移形成物资的累积，物资的最终累积量即为供应商通过储备努力获得的联储库存。假定供应商b在t时刻储备的物资为 θ b φ b ( t )，记t时刻的物资累积量为 q ( t )， λ为储备过程中的物资损耗量［15］。则 q ( t )随着时间的变化状态可表示为微分方程的形式： d q ( t ) d t = θ b φ b ( t ) - λ q ( t )，考虑到供应商a和供应商b合作储备应急物资，与上述推理过程类似，可以得到t时刻联储库存物资的总累积量 Q s ( t )为：
d Q s ( t ) d t = θ a φ a ( t ) + q t - λ Q s t
本文作用的变量符号及含义如表1所示。
表1 变量符号及含义
符号 符号含义 符号 符号含义
σ i 供应商成本补贴比例， σ a表示供应商a对供应商b的补贴， σ b表示供应商b对供应商a的补贴， i = a , b。决策变量 φ i ( t ) t时刻供应商 i的储备努力，与机会主义行为倾向负相关， i = a , b。决策变量
τ 政府的储备补贴比例。决策变量
Q s t t时刻政企联合储备应急物资库存总量 q t t时刻供应商b参与储备的应急物资数量
Q m 联合储备应急物资库存规定保有量 Q g 政府自储备应急物资库存量
Q n 应急物资的实际需求量 p h 灾害发生概率
p h j 灾害发生后三种情景的条件概率， j = 1,2 , 3 p s 灾害发生时，物资储备足以应对需求的可能性， p s = 1 - p h 3
α 减灾效益系数，表明单位储备物资可消除的经济损失 E Q s 供应商储备收益，为多个情景下储备收益的期望值
η 奖惩系数，单位物资的奖励或惩罚金额 μ i 努力成本系数， i = a , b
β 政府从联储库存中采购物资的价格 u 供应商b储备单位物资所获取收益
θ i 储备转化系数，供应商储备努力转化为实际储备的能力 γ 贴现率
λ 物资损耗系数，表示因运输等原因导致的储备量损失 ν 残值收益比， ν ∈ 0,1

2.3 CS契约与RS&BS契约的决策内容与顺序

本文研究了一个由政府（g）、核心供应商（a）与节点供应商（b）联合储备应急物资的供应系统。政府与供应商的决策过程如图1所示，图1中虚线表示储备收益的流动过程，实线表示各参与主体的决策过程，序号表示决策顺序。
图1 CS契约与RS&BS契约下政企各方决策过程
具体决策过程描述如下：
（1）政府的决策内容与顺序为：政府规定供应商需储备不低于最低保有量 Q m单位的联储库存物资，在物资储备阶段，政府与供应商协商制定联储库存物资的采购价格 β，并决定给予供应商 τ比例的储备补贴，此后，通过比较 Q s与 Q m考察供应商履约状况，以奖惩系数 η对供应商进行奖惩。灾害发生后，政府优先调用自身储备物资 Q g，当自身储备不足时，根据剩余物资需求以价格 β从联储库存中采购物资，并在契约期满后以 ν β价格对剩余物资做残值处理。
（2）CS契约下，供应商的决策内容与顺序如图1（a）所示，具体描述为：①供应商a作为政府的跟随方，根据政府所提供的储备补贴 τ、奖惩系数 η及自身成本、储备能力等因素决定努力水平 φ a和对供应商b的成本分担比例 σ a，同时，根据供应商b在联储库存中的储备量支付费用；供应商b作为供应商a的跟随者，根据供应商a的努力水平及成本分担比例，决定自身努力水平 φ b。
（3）RS&BS契约下，供应商的决策内容与顺序如图1（b）所示，具体描述为：不同于CS契约，RS&BS契约下供应商b作为供应商a的跟随者，不仅要根据供应商a的努力水平与成本分担比例决定自身努力水平 φ b，还要根据所获得的收益分成来决策对供应商a的成本分担比例 σ b。

2.4 供应商储备收益分析

供应商的储备收益来自政府对联储库存中物资的采购，而政府的采购策略由不同情境下的物资需求及自身储备情况所决定，因此，有必要结合不同情境对储备收益展开分析。具体如下：（1）灾害不发生，政府不采购联储库存物资，并在契约期满时支付联储库存全部物资的出清费用，此时，储备收益为： c h ¯ = ν β Q s；（2）灾害发生时，可进一步分为三种情境，分别用 c h 1、 c h 2、 c h 3表示这三种情境下的储备收益：① Q g ≥ Q n，政府自储库存可以满足物资需求，此时，政府不采购物资，并在契约期结束后支付联储库存的出清费用， c h 1 = ν β Q s；② Q g ≤ Q n ≤ Q g + Q s，政府自储库存无法满足全部物资需求，需要采购联储库存的部分物资，此时， c h 2 = β Q n - Q g + ν β Q s - Q n + Q g；③ Q g ≤ Q n ≤ Q g + Q s，政府自身储备与联储库存无法满足物资需求，政府将采购联储库存中的全部物资，此时， c h 3 = β Q s。用 p h表示灾害概率，分别用 p h 1、 p h 2、 p h 3表示灾害发生后出现以上三种情境的条件概率，则供应商储备收益的期望值为：
E Q s = 1 - p h c h ¯ + p h p h 1 c h 1 + p h 2 c h 2 + p h 3 c h 3
令 p h 2 = 1 - p h 1 - p h 3，整理式（2）得： E Q s = β v + p h 3 p h 1 - v Q s + p h β 1 - ν Q g - Q n p h 1 + p h 3 - 1。为简化书写，记 ρ = v + p h 3 p h 1 - v。为方便后文分析，定义 p s = 1 - p h 3，表示灾害发生时，物资储备足以应对灾害的可能性。

3 模型构建与求解

3.1 储备成本分担契约（CS）下的政企联合储备模型构建与求解

3.1.1 CS契约下的政企联合储备模型构建

政府以减灾效益最大化及成本控制为目标。 α Q s表示应急储备带来的减灾效益。政府成本包括物资采购支出、对供应商的补贴支出以及奖惩支出。物资采购支出等于供应商的储备收益 E Q s，已在上文中进行了论述；补贴支出是指政府针对供应商的储备成本给与 τ比例的储备补贴，表示为 τ C φ a；奖惩支出指当联储库存 Q s低于规定的最低保有量 Q m时，根据所缺数量 Q m - Q s，以单位罚金 η进行处罚，反之，当 Q s > Q m，以单位奖金 η奖励超出部分。因此， t时刻政府的收益函数为：
Π g τ = ∫ 0 ∞ e - γ t { α Q s t - E Q s t - τ C φ a t + η Q m - Q s t } d t
为书写简洁，下文省略 t。
供应商以收益最大化及储备成本最小化为目标。CS契约下，供应商a作为供应主导方，独享政府提供的储备收益、补贴收益及奖惩收益，但需根据供应商b的储备数量，按量支付其储备费用 u q，并为其分担的 σ a比例的储备成本。与之对应，供应商b除获取储备费用 u q外，还需承担 1 - σ a比例的储备成本。综上，CS契约下， t时刻供应商a和供应商b的收益函数分别为：
Π a φ a , σ a = ∫ 0 ∞ e - γ t { E Q s - 1 - τ C φ a - u q - η Q m - Q s } d t
Π b φ b = ∫ 0 ∞ e - γ t u q - 1 - σ a C φ b d t

3.1.2 CS契约下的政企联合储备模型求解

命题1 供应商采取CS契约时，政府的最优储备补贴比例 τ C、供应商的最优努力策略 φ i C及最优成本分担比例 σ a C分别为：
τ C = 2 α - 3 η - 3 β ρ 2 α - η - β ρ
φ a C = 2 α - η - β ρ 2 μ a γ + λ θ a  ，   φ b C = 2 η + β ρ - u γ + λ 2 μ b γ + λ 2 θ b
（7）
σ a C = 2 η + β ρ - 3 u γ + λ 2 η + β ρ - u γ + λ
证明：通过逆向归纳法和最优控制理论求解此博弈的斯塔尔伯格均衡。假定存在连续有界的微分收益函数 Π b ≥ 0满足以下HJB（Hamilton-Jacobi-Bellman）方程：
γ ⋅ Π b = m a x { u q - 1 - σ a C φ b + ∂ Π b ∂ Q s θ a φ a + q - λ Q s + ∂ Π b ∂ q θ b φ b - λ q }
为书写简洁，记 Π g Q ' = ∂ Π g ∂ Q s、 Π g q ' = ∂ Π g ∂ q、 Π a Q ' = ∂ Π a ∂ Q s、 Π a q ' = ∂ Π a ∂ q、 Π b Q ' = ∂ Π b ∂ Q s、 Π b q ' = ∂ Π b ∂ q。
对式（9）求关于 φ b的一阶最优条件，得：
φ b = θ b 1 - σ a μ b Π b Q '
供应商a基于完全信息可以理性推断出供应商b的努力水平 φ b，并据此决策自身的努力水平 φ a及成本分担比例 σ a，因此供应商a的HJB方程为：
γ ⋅ Π a = m a x { E Q s - 1 - τ C φ a - u q - η Q m - Q s + Π a Q ' θ a φ a + q - λ Q s + Π a q ' θ b φ b - λ q } d t
将式（10）代入式（11），并分别求 φ a、 σ a的一阶最优条件，可得：
φ a = θ a 1 - τ μ a Π a Q ' σ a = 2 Π a Q ' - Π b Q ' / 2 Π a Q ' + Π b Q '
与供应商a类似，政府可以通过推断供应商a的理性反应，决策最优的补贴系数，政府的HJB方程为：
γ ⋅ Π g = m a x { α Q s - E Q s - τ C φ a + η Q m - Q s + Π g Q ' θ a φ a + q - λ Q s + Π g q ' θ b φ b - λ q } d t
将式（12）代入式（13）并求 τ的一阶最优条件得：
τ = 2 Π g Q ' - Π a Q ' / Π a Q ' + 2 Π g Q '
将式（10）、式（12）、式（14）代入式（9）、式（11）、式（13）。参考Saha等［16］的研究，假设各方的收益函数 Π g 、 Π a 、 Π b 关于 Q s和 q的线性解析式分别为：
Π g = m 1 Q s + m 2 q + u m 1 , m 2 Π a = n 1 Q s + n 2 q + u n 1 , n 2 Π b = h 1 Q s + h 2 q + u h 1 , h 2
其中， m 1、 m 2、 n 1、 n 2、 h 1、 h 2均为常数，将式（15）分别求关于 Q s、 q的一阶偏导，并将结果连同式（10）、式（12）、式（14）代入式（3）、式（4）及式（5）中，可得：
γ ⋅ Π g = α - η - β ρ - m 1 λ Q s + m 1 - m 2 λ q      + η Q m - m 1 n 1 θ a 2 μ a s 1 - m 2 h 2 θ b 2 μ b s 2 + 1      - n 1 θ a 2 2 m 1 - n 1 2 μ a 2 m 1 + n 1 s 1 2 γ ⋅ Π a = η + β ρ - n 1 λ Q s + n 1 - u - n 2 λ q      - η Q m - n 1 θ a 2 μ b s 1 + n 1 θ a 2 s 1 2 μ a s 1 2 - n 2 h 2 θ b 2 μ b s 2      - h 1 θ b 2 2 n 2 - h 2 2 μ b 2 n 2 + h 2 s 2 2 γ ⋅ Π b = - h 1 λ Q s + h 1 + u - h 2 λ q - h 2 θ b 2 μ b s 2      + h 2 θ b 2 s 2 2 μ b s 2 2 - n 1 h 1 θ a 2 μ a s 1 s 1 = 2 m 1 - n 1 2 m 1 + n 1 - 1 , s 2 = 2 n 2 - h 2 2 n 2 + h 2 - 1
可由式（16）中的各式联立解得：
m 1 = α - η - β ρ γ + λ， m 2 = α - η - β ρ γ + λ 2，
n 1 = η + β ρ γ + λ， n 2 = η + β ρ γ + λ 2 - u γ + λ， h 1 = 0，
h 2 = u γ + λ
将 m 1、 m 2、 n 1、 n 2、 h 1、 h 2的值代回式（16）中，即可求解得到命题1中的政企最优策略 τ C、 φ i C、 σ a C以及最优收益函数 Π g C、 Π a C、 Π b C，命题1可证。
参考Cellini等［17］对于灾害应急效率轨迹的研究，可进一步得到CS契约下联储库存 Q s C t、供应商努力水平 φ a C t及 φ b C t在时间维度上的轨迹：
Q s C t = Q ∞ C + 1 γ + λ q 0 - q ∞ C e - γ t      + Q 0 - Q ∞ C + 1 γ + λ q 0 - q ∞ C e - γ t Q ∞ C = 1 2 γ + λ 2 α - η - β ρ μ a θ a 2      + 2 η + β ρ - u γ + λ μ b γ + λ θ b 2 q ∞ C = 2 η + β ρ - u γ + λ 2 μ b γ + λ 2 θ b 2 φ a C t = φ a C 1 - e - γ T - t , φ b C t = φ b C 1 - e - γ T - t 2
其中， Q 0、 q 0分别为 Q s t及 q t初始值。

3.2 收益分成&双边成本分担契约（RS&BS）下的政企联合储备模型构建与求解

3.2.1 RS&BS契约下的政企联合储备模型构建

当供应商采取RS&BS契约后，供应商的目的仍是实现自身收益的最大化。此时，供应商a不再根据供应商b的储备数量支付其费用，而是向其提供 1 - ω比例的储备及奖惩收益分成，不同于CS契约中，供应商a单边分担供应商b的储备成本，RS&BS契约中引入了双边补助机制，也即供应商b也为供应商a分担 σ b比例的储备成本［13］，此举旨在通过双边补助机制的灵活性使供应链能在更大范围内实现协调，后文将对此进行论述。综上，RS&BS契约下， t时刻供应商a和供应商b的收益函数分别为：
Π a ( φ a , σ a ) = ∫ 0 ∞ e - γ t { ω ( E ( Q s ) - η ( Q m - Q s ) ) - ( 1 - τ - σ b ) C ( φ a ) - σ a C ( φ b ) } d t
类似地， t时刻供应商b的收益函数为：
Π b φ b , σ b = ∫ 0 ∞ e - γ t { 1 - ω ( E Q s - η ( Q m - Q s ) ) - 1 - σ a C ( φ b ) - σ b C ( φ a ) } d t
t时刻政府的收益函数同式（3）。

3.2.2 RS&BS契约下的政企联合储备模型求解

命题2 供应商采取RS&BS契约时，政府的最优储备补贴比例 τ R、供应商的最优努力策略 φ i R及最优成本分担比例 σ i R分别为：
τ R = 4 α + ω - 6 η + β ρ 4 α - 2 + ω η + β ρ
φ a R = 4 α - ω + 2 η + β ρ 4 μ a γ + λ，
φ b R = 1 + ω η + β ρ 2 μ b γ + λ 2 θ b
σ a R = 3 ω - 1 ω + 1， σ b R = 4 - 6 ω η + β ρ 4 α - 2 + ω η + β ρ
证明：同样采取逆向归纳法及最优控制理论求解此斯塔尔伯格博弈的均衡策略，证明过程与CS契约的求解过程类似，因此不再赘述，命题2得证。
进一步，可求得此时政企各方的最优收益函数 Π g R、 Π a R、 Π b R。此外，还可求得联储库存 Q s R t、供应商努力水平 φ a R t、 φ b R t的时间轨迹：
Q s R t = Q ∞ R + 1 γ + λ q 0 - q ∞ R e - γ t      + Q 0 - Q ∞ R + 1 γ + λ q 0 - q ∞ R e - γ t Q ∞ R = 1 γ + λ 4 α - ω + 2 η + β ρ 2 μ a θ a 2      + 1 + ω η + β ρ μ b γ + λ θ b 2 q ∞ R = 1 + ω η + β ρ 2 μ b γ + λ 2 θ b 2 φ a R t = φ a R 1 - e - γ T - t φ b R t = φ b R 1 - e - γ T - t 2

4 模型结果对比分析

命题3 （1）使CS契约生效的可执行采购价格区间为： 3 u γ + λ 2 ρ - η ρ ≤ β ≤ 2 α 3 ρ - η ρ；使RS&BS契约生效的可执行采购价格范围为： β ≤ 4 α 6 - ω ρ - η ρ；（2）政府对于供应商的最优补贴总有 τ R ≥ τ C；当 β ≤ u γ + λ ρ 1 - ω - d ρ时，有 σ a R ≥ σ a C成立，否则，有 σ a R < σ a C成立；（3）任意条件下，总有 φ a R < φ a C成立，当 σ a R ≥ σ a C时，有 φ b R ≥ φ b C成立，否则，有 φ b R < φ b C成立；（4）当 β ≥ 1 K 2 μ a θ b 2 ( u γ + λ - η 1 - ω ) - μ b θ a 2 ω η ( γ + λ ) 2 μ a θ b 2 ( 1 - ω ) + μ b θ a 2 ω ( γ + λ )时， Q s C ≥ Q s R，否则， Q s C < Q s R。
证明：根据式（6）~式（8）、式（20）~式（22）可得：
τ R - τ C = 4 ω η + ρ β α - η - ρ β 2 α - η - ρ β 2 + ω η + ρ β - 4 α c
σ a R - σ a C = 3 ω - 1 ω + 1 - 2 η + ρ β - 3 u γ + λ 2 η + ρ β - u γ + λ
φ a R - φ a C = - θ a ω η + β ρ 4 μ a γ + λ
φ b R - φ b C = u γ + λ + ω - 1 η + β ρ 2 μ b γ + λ 2 θ b
Q s R - Q s C = Δ Q - Δ Q e - γ t Δ Q = u γ + λ + ω - 1 η + β ρ 2 μ b γ + λ 2 θ b 2     - ω η + β ρ 4 μ a γ + λ θ a 2
为使得CS契约可以生效，需要满足CS契约下的均衡策略均有意义，因此，可得： 1 ≥ τ C = 2 α - 3 η - 3 β ρ 2 α - η - β ρ ≥ 0， φ a C = 2 α - η - β ρ 2 μ a γ + λ θ a ≥ 0， φ b C = 2 η + β ρ - u γ + λ 2 μ b γ + λ 2 θ b ≥ 0  ， 1 ≥ σ a C = 2 η + β ρ - 3 u γ + λ 2 η + β ρ - u γ + λ ≥ 0，联立上述不等式可以得到使CS契约生效的采购价格范围为 3 u γ + λ 2 ρ - η ρ ≤ β ≤ 2 α 3 ρ - η ρ，同理可证RS&BS的采购定价范围，命题3（1）可证。
由命题3（1）可知：
2 α - η - β ρ ≥ 0， α - η - ρ β ≥ 0， 2 α - η - ρ β ≥ 0， 2 + ω η + ρ β - 4 α ≤ 0，因此，可推知：
τ R - τ C = 4 ω η + ρ β α - η - ρ β 2 α - η - ρ β 2 + ω η + ρ β - 4 α ≤ 0，命题3（2）可证。类似地，可证明命题3（3）、命题3（4）同样成立，命题3得证。
由命题3可得到以下启示：
（1）由命题3（1）可知：由于 1 / 3 < ω < 2 / 3，易得 2 α 3 ρ - η ρ < 4 α 6 - ω ρ - η ρ，因此，RS&BS契约相比于CS契约具有更大的可执行采购价格区间，RS&BS契约下，供应商可以接受政府更灵活的定价策略，表明：通过引入RS&BS契约的双边补助机制使得政企之间更有机会实现供应链的协调，这与文献［14］观点一致，后文将通过数值仿真对此进行验证。
（2）由命题3（2）可知，RS&BS契约相比于CS契约需要政府提供更高的补贴，这是由于，相较于CS契约，RS&BS契约下的供应商a失去了 1 - ω比例的储备及奖惩收益，若此时还要承受同等的储备成本，则有可能造成自身的收益受损而退出合作。
（3）结合命题3（2）、命题3（3）可知：相比于CS契约，RS&BS契约下的供应商a倾向于降低自身储备努力（ φ a R < φ a C），转而由供应商b承担更多的储备任务，但当物资采购价格低于一定阈值时（ β ≤ u γ + λ ρ 1 - ω - η ρ），供应商a须提高对供应商b的成本分担比例（ σ a R ≥ σ a C），以避免供应商b因过高的储备成本而减少努力，诱发机会主义行为（ φ b R < φ b C）。
（4）由命题3（4）可知：CS契约和RS&BS契约下的联储库存储备量存在一个关于采购价格的临界值 β = 1 ρ 2 μ a θ b 2 ( u γ + λ - η 1 - ω ) - μ b θ a 2 ω η γ + λ 2 μ a θ b 2 1 - ω + μ b θ a 2 ω γ + λ，当采购价格高于该值时，CS契约在物资储备数量上存在优势，否则，RS&BS契约提供应急物资储备量更高。这说明，CS契约与RS&BS契约在储备量上各自具有关于采购价格的优势区间。因此，政府应根据自身物资需求，结合供应商合作形式，理性制定采购价格。

5 数值分析

下面通过数值仿真，进一步验证本文提出的命题。借鉴张琳等［6］的研究成果，参数设置如下： T = 50、 α = 10、 θ a = 1.5、 θ b = 2、 ω = 0.5、 u = 10.5、 Q m = 250、 μ a = 2、 μ b = 2.5、 γ = 0.1、 λ = 0.15。计算可得不同契约形式下的均衡策略和联储库存物资量（见表2），命题1、命题2得到验证。进一步可计算得到：可使CS契约生效的可执行采购价格范围为（17.50，36.32），可使RS&BS契约生效的可执行范围为（0，40.50），使 σ a R ≥ σ a C成立的采购价格区间为 β ≤ 26.55，使 Q s R ≥ Q s C成立的采购价格区间为 β ≤ 23.63，命题3得到验证。后续通过分析采购价格、时间及灾害概率等重要参数对均衡策略、联储库存的时间轨迹的影响，验证命题3得到的部分结论，并据此提炼管理启示。
表2 不同契约下的均衡策略及联储库存
策略 φ a φ b τ σ a σ b Q s T
CS 23.55 38.24 0.45 0.12 — 111.74
RS&BS 21.93 41.28 0.56 0.33 0.15 115.40
（1）由图2（a）可知：政府最优补贴比例 τ随着采购价格 β增大而减小，且RS&BS契约下的最优补贴比例 τ R始终高于CS契约。这是由于，政府出于经济理性，在提高补贴强度的同时，会调低采购价格以避免自身成本的失控，反之亦然。因此，政府应遵从采购价格与储备补贴“此消彼长”的特点，合理制定“高价低补贴”或“低价高补贴”的激励策略。此外，相较于CS契约，政府需为RS&BS契约下的供应商提供更高的储备补贴。
图2 决策变量变化趋势
（2）由图2（b）可知：CS契约下，供应商a的最优成本分担比例 σ a C随着 β增加而增加，在RS&BS契约下则维持不变。且当 β < 17.5时， σ a C < 0，此时契约失效。这表明，CS契约存在一个价格门槛（ β = 17.5），当物资采购价格大于该值时，供应商a愿意以分担成本的形式鼓励其他供应商参与合作，当小于该值时，供应商a会因无利可图而终止合作。而在RS&BS契约下，只要保证供应商内部收益分配合理（ 1 / 3 < ω < 2 / 3），双方可始终维持合作关系。说明CS契约下供应商a的成本分担策略更加受到外部采购价格的约束，而RS&BS契约下该决策仅取决于供应商内部的收益分配。因此，当供应商采取CS契约时，政府应格外重视所执行的采购价格，避免因过度压价造成核心供应商一方利益受损。
（3）由图2（c）可知： σ b R随着 β增加而增加。这是由于，RS&BS契约下供应商b享有固定比例的收益分成，因此供应商b的利润随着 β增加而增加，使得供应商b有意愿通过增加对供应商a的成本分担比例来刺激其储备更多的应急物资，这也是RS&BS契约可以生效的原因。
（4）由图2（d）、图2（e）、图2（f）可知：供应商的最优努力水平随时间推移而下降，并在契约期结束时下降为零。此外，对于任意采购价格 β，总有 φ a C ≥ φ a R成立。供应商b的努力程度则视供应商a的成本分担比例而定，分担比例越高，供应商b的努力水平越高，这验证了命题3（2）、命题3（3）的部分结论。
（5）由图3（a）可知：政府的收益 Π g随着采购价格 β的增加而呈现“倒U型”分布。CS契约与RS&BS契约下，使政府收益最大化的采购价格分别为 β = 26.96、 β = 21.81。对政府而言，CS契约下执行的采购定价应高于RS&BS契约，这意味着，供应商不同的合作形式也会反向影响政府的定价策略，因此，将代储供应商间的合作关系纳入政企代储问题的研究中是合理且必要的，这是以往文献中鲜有探讨的。由图3（b）、图3（c）可知：供应商的收益均随着 β增大而增大，因此，政府在合理范围内提高采购价格可以刺激供应商的参与积极性。
图3 采购价格对收益的影响
（6）进一步分析供应链的协调性，结合图3（a）、图3（b）、图3（c）可知：使得政府的在不同契约下收益最大的采购价格并不一致，假设政府坚持以自身的收益最大化出发，执行采购价格 β = 21.81或 β = 26.96，此时供应商a和供应商b均难以就契约的形式达成一致，供应链无法实现协调。RS&BS契约则可以提供一个柔性的采购价格执行区间（ 22.41 ≤ β ≤ 24.61），使得此区间的供应商均会自发地选择参与RS&BS契约，这一选择同样对政府有利，而CS契约则无法在该场景中实现供应链的协调。这表明，相较于经典的单边成本分担契约，RS&BS契约通过对双边补偿及收益分成机制进行组合，提高了对供应链的协调能力，这也验证了命题3（1）的结论。
由图4可知：
图4 联合储备库存量变化趋势
（7）在图4（a）中进一步分析两种契约形式在应用场景上的差异，将图中两曲面交线在X-Y坐标平面上的投影与X轴、Y轴所围成的区域称为 Z L，其余区域称为 Z H。 Z L区域灾害发生概率较低（ p h < 0.6），且应急物资充足（ p s > 0.4），可以刻画低灾害风险时期的场景，与之对应， Z H可表示高灾害风险时期的场景。总体而言， Z L区域内，RS&BS契约下的联储库存更高，且变化平稳； Z H区域内，CS契约下的库存量更高，且由曲面的曲度可知，灾害发生概率越高，应急物资约紧缺，则库存增幅越大。这表明，对政府而言，在低灾害风险期引导供应商选择RS&BS契约更有助于将库存维持在一个稳定的安全保有量（ Q s R ≥ Q s C），而在灾害高风险期则可通过CS契约刺激供应商尽可能多地储备应急物资（ Q s C > Q s R）。供应商也可根据不同场景理性地选择RS&BS和CS契约，确保在高风险期的高效储备及快速响应，在低风险期维持企业的可持续经营。
（8）由图4（b）、图4（c）可知：两种契约机制下联储库存均随着时间递增直到维持到一个稳定值，且稳定值与供应商b的储备量 q均不受联储库存初始值 Q 0的影响。这说明，尽管供应商的较高的库存初始值会降低其储备效率（同一时刻A点斜率高于B点斜率），但只要执行同一契约形式，联储库存最终会趋于同一个稳定值，这意味着，在现实市场中，供应商之间的长期稳定的契约关系有利于确保供应链系统的稳定性。

6 结语

本文研究了一个由政府和两个异质性供应商联合储备应急物资的供应系统。为激励供应商参与合作，并改善供应链的协调性，本文设计了储备成本单边分担契约（CS）以及具有储备及奖励收益分成的双边成本分担契约（RS&BS），研究了政府的最优补贴策略、供应商的努力策略、分担策略及联储库存的时间轨迹，并结合数值仿真，分析了采购价格等参数对策略选择的影响以及两类契约的各自优势与最佳应用场景。基于上述研究，得到以下结论：
（1）相比与经典CS契约，RS&BS契约通过引入收益分成及双边补偿机制，使得政府的可执行采购价格区间由CS契约的 17.5 ≤ β ≤ 36.32拓展到了 β ≤ 40.5，且不存在使CS契约生效所需的价格门槛（ β ≥ 17.50），政府和供应商得以在更灵活的价格范围内达成合作。此外，RS&BS契约具备更好的供应链的协调能力，在CS契约无法协调的场景下，可以提供一个柔性采购价格执行区间（ 22.41 ≤ β ≤ 24.61），实现政企多方共赢。
（2）供应商的合作形式也会反向影响政府的定价策略。RS&BS契约下，核心供应商的分担策略仅取决于供应商内部的收益分配，而在CS契约下，其分担策略则受到外部采购价格制约，一旦低于应急物资的价格门槛（ β = 17.50），核心供应商会因利益受损而终止合作。因此，当供应商采取CS契约时，政府应格外重视所执行的采购价格，避免因过度压价造成企业合作关系的瓦解。
（3）CS契约与RS&BS契约拥有各自最佳的应用场景。灾害高风险期（ p h > 0.6， p s < 0.4），CS契约对增加联储库存物资数量和储备效率更加有效。但当灾害状态得到控制，灾害发生概率较低（ p h < 0.6）且应急物资较为充足时（ p s > 0.4），RS&BS契约更有助于将库存维持在一个稳定的安全保有量。此外，联储库存的时间轨迹表明，只要供应商长期执行同一契约形式，联储库存最终会趋于同一个稳定值，因此，供应商之间建立长期的契约关系有利于确保供应链系统的稳定性。
基于上述模型分析所得到的理论结果，将其映射到现实市场中，提出以下与现实情景相结合的管理启示：疫情期间，国内应急部门与大型代储企业签订应急物资战略合作协议，代储企业进行部分实物储备，并联合美团等大型电商物流企业以补贴的形式建立可快速响应的供货渠道及配送网络作为能力储备（单边补助机制CS）。此时，实施CS契约可以很好地提高物资供货效率。但随着疫情得到控制，救援物资的需求降低，而专门的配送网络及供货渠道又需要可持续性的投入，代储企业容易出现懈怠等投机行为。故在此时，RS&BS契约更有优势，代储厂家通过与电商物流企业约定分享一定比例政府应急采购时的价格溢出（收益分成机制RS），以此换取供货渠道及配送网络维持成本的部分减免（双边补助机制BS），使得应急供应链进一步得到协调，实现在低灾害风险下的常态化运行。
在后续研究中，可结合应急储备物资的不同类型进行更为深入的探讨。本文仅讨论了政府与两个供应商的决策策略，后续可进一步推广到政府与多个代储供应商的联合决策。

References

Publishing order | Descend order by publishing year | Descend order by cited within
1
扈衷权， 田军， 冯耕中. 基于数量柔性契约的双源应急物资采购定价模型［J］. 中国管理科学， 2019， 27（12）：100-112.

Hu Z Q， Tian J， Feng G Z. Pricing model of dual-source emergency supplies procurement based on quantitative flexible contract［J］. Chinese Journal of Management Science， 2019， 27（12）：100-112.

2
吴勇刚，王熹徽，梁樑.灾害应对策略的评估模型及分类框架研究［J］.系统工程理论与实践，2015，35（5）：1144-1154.

Wu Y G， Wang X H， Liang L. Research of evaluation model and classification framework on disaster response strategy［J］. Systems Engineering Theory & Practice， 2015， 35（5）： 1144-1154.

3
Zhang J H， Sun X Q， Zhu R， et al. Solving an emergency rescue materials problem under the joint reserves mode of government and framework agreement suppliers［J］. Plos One， 2017， 12（10）：e0186747.

4
高晓宁，田军，冯耕中.政府委托下应急物资生产能力代储系统激励契约设计［J］.管理工程学报，2019，33（1）：182-188.

Gao X N， Tian J， Feng G Z. Design of an incentive contract on the agent emergency supplies productivity capacities reservation system being consigned by local government［J］. Journal of Industrial Engineering and Engineering Management， 2019， 33（1）： 182-188.

5
张琳，田军，杨瑞娜，等.数量柔性契约中的应急物资采购定价策略研究［J］.系统工程理论与实践，2016，36（10）：2590-2600.

Zhang L， Tian J， Yang R N， et al. Emergency supplies procurement pricing strategy under quantity flexible contract［J］. Systems Engineering Theory & Practice， 2016， 36（10）： 2590-2600.

6
张琳，田军，冯耕中.价格柔性契约下政府应急物资采购协调机制研究［J］.中国管理科学，2017，25（11）：158-167.

Zhang L， Tian J， Feng G Z. Coordination mechanism of government emergency supplies procurement under price flexibility contract［J］. Chinese Journal of Management Science， 2017， 25（11）： 158-167.

7
刘阳，田军，冯耕中.基于数量柔性契约与Markov链的应急物资采购模型［J］.系统工程理论与实践，2020，40（1）：119-133.

Liu Y， Tian J， Feng G Z. Government’s relief supplies procurement model based on quantity flexible contract and Markov chain［J］. Systems Engineering Theory & Practice， 2020， 40（1）： 119-133.

8
刘阳，田军，冯耕中，等.基于期权契约的政企联合储备应急物资模型与利润分配机制研究［J］.中国管理科学，2020，28（8）：162-171.

Liu Y， Tian J， Feng G Z， et al.Study on the model and profit distribution mechanism of government-enterprise joint reserve emergency supplies based on option contract ［J］. Chinese Journal of Management Science， 2020， 28（8）： 162-171.

9
周艳菊， 鲍茂景， 陈晓红，等. 基于公平关切的低碳供应链广告合作-减排成本分担契约与协调［J］. 中国管理科学， 2017，25（2）：121-129.

Zhou Y J， Bao M J， Chen X H， et al. Co-op advertising and emission reduction cost sharing contract and coordination in low-carbon supply chain based on fairness concerns ［J］. Chinese Journal of Management Science， 2017， 25（2）：121-129.

10
刘云志， 樊治平. 考虑损失规避与产品质量水平的供应链协调契约模型［J］. 中国管理科学， 2017， 25（1）：65-77.

Liu Y Z， Fan Z P. Supply chain coordination contract model considering loss aversion and quality level ［J］. Chinese Journal of Management Science，2017，25（1）：65-77.

11
李友东， 谢鑫鹏， 营刚. 两种分成契约下供应链企业合作减排决策机制研究［J］. 中国管理科学， 2016， 24（3）：61-70.

Li Y D， Xie X P， Ying G.Study on cooperative emission reduction decision-making mechanism of supply chain enterprises under two sharing contracts［J］. Chinese Journal of Management Science， 2016， 24（3）：61-70.

12
汪勇杰， 陈通， 邓斌超.政府补贴机制下研发外包的演化博弈分析［J］.管理工程学报，2017，31（2）：137-142.

Wang Y J， Chen T， Deng B C.Evolutionary game analysis of R&D outsourcing under government subsidy mechanism ［J］. Journal of Industrial Engineering and Engineering Management， 2017， 31（2）：137-142.

13
叶同， 关志民， 陶瑾，等. 考虑消费者低碳偏好和参考低碳水平效应的供应链联合减排动态优化与协调［J］. 中国管理科学， 2017，25（10）：52-61.

Ye T， Guan Z M， Tao J， et al.Dynamic optimization and coordination of supply chain joint emission reduction considering consumers' low-carbon preference and considering the effect of low-carbon level ［J］. Chinese Journal of Management Science， 2017， 25（10）：52-61.

14
张建军， 赵晋， 张艳霞. 基于连续时间动态博弈的供应链声誉及其微分对策研究［J］. 管理工程学报， 2012， 26（1）：143-150.

Zhang J J， Zhao J， Zhang Y X.Supply chain reputation and its differential game based on continuous time dynamic game［J］.Journal of Industrial Engineering and Engineering Management， 2012， 26（1）：143-150.

15
黄欣，凌能祥.基于排放权交易与减排研发补贴的政企减排微分博弈模型［J］.系统管理学报，2020，29（6）：1150-1160.

Huang X， Lin N X. A differential game model of government and enterprise emission reduction based on emission permits trading and subsidy for emission abatement［J］. Journal of Systems Management， 2020， 29（6）： 1150-1160.

16
Saha S， Nielsen I， Moon I. Optimal retailer investments in green operations and preservation technology for deteriorating items ［J］. Journal of Cleaner Production， 2017， 140（3）：1514-1527.

17
Cellini R， Siciliani L， Straume O R. A dynamic model of quality competition with endogenous prices［J］. Journal of Economic Dynamics & Control， 2018（94） ：190-206.

Options
Outlines

/

〈 〉