1 引言
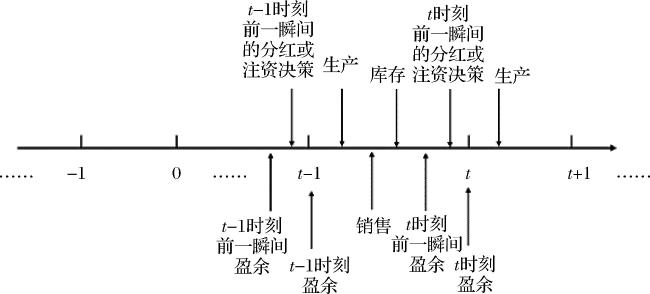
2 问题描述
3 有限时间内的生产优化
4 无时间限制的生产优化
5 数值计算
表1 联合分布 |
| 单位售价 | 单位成本 | 需求量 | 概率 |
|---|---|---|---|
| 1.2 | 3 | 1 | 0.07 |
| 1.2 | 3 | 2 | 0.07 |
| 1.2 | 3 | 3 | 0.09 |
| 1 | 2.8 | 4 | 0.11 |
| 1 | 2.8 | 5 | 0.11 |
| 1 | 2.8 | 6 | 0.12 |
| 0.8 | 2.6 | 7 | 0.1 |
| 0.8 | 2.6 | 8 | 0.09 |
| 0.8 | 2.6 | 9 | 0.09 |
| 0.6 | 2.4 | 10 | 0.06 |
| 0.6 | 2.4 | 11 | 0.05 |
| 0.6 | 2.4 | 12 | 0.04 |
表2 最优生产策略 |
|
g | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | …… |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1.2 | 8 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | …… |
| 1 | 10 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | …… |
| 0.8 | 12 | 12 | 10 | 10 | 10 | 9 | 9 | 9 | 9 | 5 | 5 | 4 | 2 | 2 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | …… |
| 0.6 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 13 | 13 | 13 | 11 | 11 | 8 | 8 | 8 | 7 | 6 | 4 | 4 | 3 | 2 | 1 | 0 | …… |
表3 最优值函数 随 的变化 |
| 0 | 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|---|
| 90.4834 | 91.4615 | 92.4996 | 93.4767 | 94.4560 | 95.4786 | |
| 92.6786 | 93.6563 | 94.6847 | 95.6673 | 96.6447 | 97.6596 | |
| 96.1290 | 97.1046 | 98.1151 | 99.0959 | 100.0731 | 101.0743 | |
| - | 103.3881 | 104.3789 | 105.3806 | 106.3584 | 107.3439 | |
| 6 | 7 | 8 | 9 | 10 | ||
| 96.4572 | 97.4376 | 98.4574 | 99.4374 | 100.4174 | ||
| 98.6407 | 99.6193 | 100.6322 | 101.6122 | 102.5922 | ||
| 102.0545 | 103.0331 | 104.0323 | 105.0123 | 106.7644 | ||
| 108.3382 | 109.3170 | 110.2995 | 111.2919 | 112.2719 |
表4 最优值函数 随 的变化 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
|---|---|---|---|---|---|---|---|---|
| - | - | - | - | - | - | 91.0087 | 96.1625 | |
| - | - | - | - | - | 92.6786 | 93.6563 | 94.6847 | |
| - | - | 93.6321 | 94.4922 | 95.3226 | 96.1474 | 96.9537 | 97.7378 | |
| 97.2150 | 97.9784 | 98.7196 | 99.4349 | 100.1324 | 100.8169 | 101.4909 | 101.4909 | |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 | …… | |
| 93.3081 | 94.4560 | 95.6026 | 96.6447 | 97.5911 | 98.4462 | 99.2717 | …… | |
| 95.6673 | 96.6447 | 97.6596 | 98.6407 | 99.5834 | 100.4349 | 101.2567 | …… | |
| 98.5011 | 99.2717 | 100.0731 | 100.8920 | 101.6213 | 102.4191 | 103.2154 | …… | |
| 102.1435 | 102.7783 | 103.3881 | 103.9607 | 104.5910 | 105.2120 | 105.7365 | …… |
表5 最优值函数 随 的变化 |
| 1.2 | 1.0 | 0.8 | 0.6 | |
|---|---|---|---|---|
| 102.0545 | 102.0545 | 102.0545 | 102.9678 | |
| 97.4376 | 97.6596 | 97.6596 | - | |
| 101.5715 | 101.5715 | 101.6213 | 103.2372 | |
| 94.6245 | 95.6673 | 95.6673 | - | |
| 89.6899 | 91.6324 | 93.9339 | 97.2150 |
表6 各期的最优生产决策 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 7 | |
| 6 | 6 | 6 | 6 | 6 | 6 | 6 | 5 | 5 | 2 | |
| 9 | 9 | 9 | 6 | 6 | 6 | 5 | 4 | 3 | 0 | |
| 13 | 13 | 13 | 13 | 13 | 11 | 8 | 5 | 0 | 0 |
表7 不同分红边界 对应的最优值函数 |
| 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|
| 61.6535 | 78.6145 | 78.9423 | - | - | |
| * | 85.5992 | 92.9882 | 99.5517 | 106.4432 | |
| * | * | * | 85.1119 | 92.7129 | |
| * | * | * | * | 101.8918 | |
| 6 | 7 | 8 | 9 | 10 | |
| 102.9689 | 102.8506 | 102.5169 | 101.7574 | 100.8060 | |
| 107.0991 | 106.6747 | 106.1683 | 105.3574 | 104.3789 | |
| 101.0470 | 101.8460 | 101.7105 | 101.0303 | 100.0731 | |
| 103.7821 | 103.6673 | 103.4801 | 102.7901 | 101.8501 |
|
表8 无限期情形下的最优值函数 |
| (0,10,1.2) | 523.7008 |
| (2,8,1.2) | 523.3789 |
| (4,7,1.0) | 524.7476 |
| (6,6,1.0) | 525.7250 |
| (8,3,0.8) | 525.7012 |
| (10,5,0.6) | 532.8930 |