主管：中国科学院
主办：中国优选法统筹法与经济数学研究会
　　　中国科学院科技战略咨询研究院
中国管理科学

中国管理科学 >

2016 , Vol. 24 >Issue 7: 135 - 142

DOI: https://doi.org/10.16381/j.cnki.issn1003-207x.2016.07.016

论文

基于最小平方距离的区间值合作对策求解模型与方法

展开
  • 1. 福州大学经济与管理学院, 福建 福州 350108;
    2. 福建农林大学交通与土木工程学院, 福建 福州 350002

收稿日期: 2014-12-24

  修回日期: 2015-10-20

  网络出版日期: 2016-07-27

基金资助

国家自然科学基金重点项目（71231003）；国家自然科学基金资助项目（71171055）；高等学校博士学科点专项科研基金资助课题（20113514110009）；福建省社会科学规划项目（2013C024）；福建省教育厅科技项目（JA13122）

收起

Models and Method of Interval-valued Cooperative Games Based on the Least Square Distance

Expand
  • 1. School of Economics and Management, Fuzhou University, Fuzhou 350108, China;
    2. School of Traffic and Civil Engineering, Fujian Agriculture and Forestry University, Fuzhou 350002, China

Received date: 2014-12-24

  Revised date: 2015-10-20

  Online published: 2016-07-27

Fold

摘要

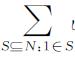现有针对联盟S特征（或支付）值表示为区间值υ（S）=[υL（S），υR（S）]的合作对策（简称区间值合作对策）的研究，多数利用区间算术（比如，区间减法）、特殊排序函数等，并在经典Shapley值基础上进行拓展。本文主要目的是发展一种基于最小平方法的n人区间值合作对策的有效求解方法。首先，利用区间值距离概念和最小平方法，建立以联盟分配与联盟支付值之差的平方和为最小的数学优化模型，据此求解确定每个局中人的区间值分配xi=[xLi, xRi]（i=1，2，…，n），可由解析公式[XL，XR]=[A-1 BL，A-1 BR]的相应分量确定，其中BL=（υL（S），υL（S），…，υL（S））T，BR=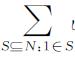（υL（S），??υL（S），…，υL（S））T，A-1=（1/2n-2）（a'ij）n×n，且a'ij=-/（n+1）（i≠j时）或n/（n+1）（i=j时）。然后，推广所导出的辅助数学优化模型，使其满足诸如有效性x（N）=υ（N）等要求，进而求解确定每个局中人的区间值分配x'i=[x'Li, x'Ri]（i=1，2，…，n），可由解析公式[X'L，X'R]=[X'L+（υL（N）-xLi）e/n，XR+（υR（N）-xRi）e/n]的相应分量确定。最后，利用一个配送联盟问题的数值实例进行验证与比较分析，说明了所提出模型与方法的有效性、实用性和优越性。文中所提出的研究模型与方法可有效避免区间值减法运算带来的计算结果不确定性扩大等不合理问题，为求解区间值合作对策提供一种新的理论视角和实用工具。

关键词： 区间值合作对策; 最小平方法; 损失函数; 配送联盟; 数学规划

本文引用格式

李登峰, 刘家财 . 基于最小平方距离的区间值合作对策求解模型与方法[J]. 中国管理科学, 2016 , 24(7) : 135 -142 . DOI: 10.16381/j.cnki.issn1003-207x.2016.07.016

Abstract

Most of the existing studies on interval-valued cooperative games in which the values of coalitions S are expressed with intervals υ(S)=[υL(S),υR(S)]are based on the interval arithmetic (e.g., interval subtraction) and ranking functions of intervals and hereby are some extensions of the classic Shapley value. The main purpose of this paper is to develop an effective method for solving n-person interval-valued cooperative games based on the least square method. Firstly, according to the concept of the distance between intervals and the least square method, an optimization mathematical model is constructed through considering that players in coalitions try to guarantee their payoffs' sums being as close to the coalitions' values as possible. 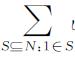Through solving the constructed optimization mathematical model, all players' interval-valued payoffs xi=[xLi, xRi] (i=1,2,…,n) can be obtained, which can be determined by the analytical formula[XL,XR]=[A-1 BL,A-1 BR], where BL=(υL(S),υL(S),…,υL(S))T,BR=(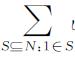υL(S),υL(S),…,υL(S))T,A-1=(1/2n-2)(a'ij)n×n, and a'ij=-/(n+1)(i≠j or n/(n+1) if i=j. Then, the auxiliary optimization mathematical model is extended so that it satisfies some conditions x(N)=υ(N) and hereby all players' interval-valued payoffs x'i=[x'Li, x'Ri] (i=1,2,…,n) are solved, which can be determined by the analytical formula[X'L,X'R]=[X'L+(υL(N)-xLi)e/n,XR+(υR(N)-xRi)e/n]. Finally, a numerical example of the dispatch coalition problem is used to conduct the validation and comparison analysis, which has shown that the proposed models and method are of the validity, the applicability, and the superiority. The models and method proposed in this paper can effectively avoid the magnification of uncertainty resulted from the subtraction of intervals and provide a new theoretical angle and suitable tool for solving interval-valued cooperative games.

Key words： interval-valued cooperative game; least square method; loss function; dispatch coalition; mathematical programming

参考文献

[1] 李登峰.模糊多目标多人决策与对策[M].北京:国防工业出版社,2003.

[2] Li Dengfeng. Lexicographic method for matrix games with payoffs of triangular fuzzy numbers[J]. International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, 2008, 16(3):371-389.

[3] Branzei R, Branzei O, Alparslan G k S Z, et al. Cooperative interval games:A survey[J]. Central European Journal of Operations Research, 2010, 18(3):397-411.

[4] 李登峰.直觉模糊集决策与对策分析方法[M].北京:国防工业出版社,2012.

[5] Han Weibin, Sun Hao, Xu Genjiu. A new approach of cooperative interval games:The interval core and Shapley value revisited[J]. Operations Research Letters, 2012, 40(6):462-468.

[6] Branzei R, Dimitrov D, Tijs S. Shapley-like values for interval bankruptcy games[J]. Economics Bulletin, 2003, 3(8):1-8.

[7] Alparslan G k S Z, Branzei R, Tijs S. The interval Shapley value:An axiomaticzation[J]. Central European Journal of Operations Research, 2010, 18(2):131-140.

[8] Mallozzi L, Scalzo V, Tijs S. Fuzzy interval cooperative games[J]. Fuzzy Sets and Systems, 2011, 165(1):98-105.

[9] Alparslan G k S Z, Miquel S, Tijs S. Cooperation under interval uncertainty[J]. Mathematical Methods of Operational Research, 2009, 69(1):99-109.

[10] Branzei R, Alparslan G k S Z, Branzei O. Cooperation games under interval uncertainty:On the convexity of the interval undominated cores[J]. Central European Journal of Operations Research, 2011, 19(4):523-532.

[11] Yu Xiaohui, Zhang Qiang. An extension of cooperative fuzzy games[J]. Fuzzy Sets and Systems, 2010, 161(11):1614-1634.

[12] Alparslan G k S Z, Branzei O, Branzei R, et al. Set-valued solution concepts using interval-type payoffs for interval games[J]. Journal of Mathematical Econo-mics, 2011, 47(4-5):621-626.

[13] Li Dengfeng. Linear programming approach to solve interval-valued matrix games[J]. Omega, 2011, 39(6):655-666.

[14] Li Dengfeng. Models and methods of interval-valued cooperative games in economic management[M]. Switzerland:Springer, 2014.

[15] Moore R E. Methods and applications of interval analysis[M]. SIAM:Studies for Industrial and Applied Mathematics, 1979.

[16] 于晓辉,张强.模糊合作对策的区间Shapley值[J].中国管理科学,2007,(Z1):76-80.
Options
文章导航

/

〈 〉